This article explains how charging a capacitor can use a lot of energy, and how your charging method has a big influence on its efficiency. It becomes more important when considering the possible super capacitors that I spoke of in the article Has the supercapacitor been invented?
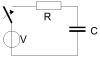
Charge Efficiency of the Capacitor
When charging and discharging a capacitor, we lose energy due to the already existing ESR (Equivalent Series Resistance). This resistance is always present since all of the charge has to be transported to the capacitor plates and, since the materials are not superconducting, it means that there is loss in transport that is converted into heat. We have a loss of energy, which we originally wanted to store or retrieve from the capacitor. We put the ESR into a scheme, and add all relevant series resistances in one R.
By choosing the charge current wisely, we can have an influence on the losses in the ESR R. There exists a simple expression that computes the losses in R:
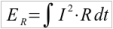
This means that the energy losses in R (ER) are the integral (= sum) of the square of the current through it, multiplied by the resitance value R itself. The sum has to be taken for the complete charging or discharging period, whichever is considered.
This loss factor we want to put in relation to the energy that is stored in the capacitor, which is:
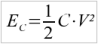
In the next chapters I will relate the results, depending on the method of charging the capacitor.
Charging with a Fixed Voltage
In the next scheme will be shown how a capacitor is charged with a fixed voltage V.
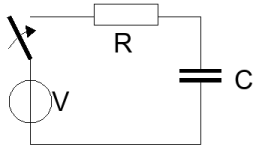
The energy stored in the capacitor
When we charge the capacitor with a fixed voltage source V, then after a time which is normally set at 5 RC, we have the capacitor charged up to V volt, and this corresponds to a stored energy amount of 1/2CV2 in the capacitor.
The Energy Losses in the ESR
To compute the losses in the ESR, we need to know the current during the charging cycle. This can be computed for the mentioned scheme:
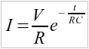
The amount of energy that we lose in the ESR R can be computed as follows:
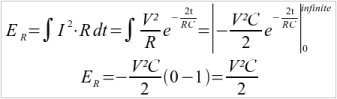
You can see that the loss in the ESR is just as big as the energy stored in the capacitor itself! This is due to the very high current that flows at the beginning of the charge cycle (just after connecting the voltage source V on the empty capacitor C).
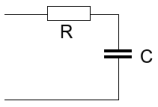
Charging with a Constant Current Source
The next scheme shows charging with a fixed current source. This current source is connected to the capacitor (with its ESR R).
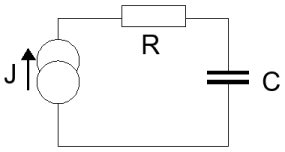
The Energy Stored in the Capacitor
When we charge the capacitor with a current source J, then, after a certain time, e.g. t1 seconds, the capacitor will be charged to V volt which gives an energy stored of 1/2CV2.
We can compute t1:
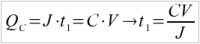
The charge in the capacitor QC is equal to the time period t1 times the constant current J during this time period. This is also equal to the capacity value C times the voltage V over the capacitor.
The Energy Losses in the ESR
To compute the amount of lost energy in R during this charge cycle, we compute with the constant value J:
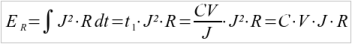
This equation is very different from the equation we found when charging with a constant voltage source.
If we now want the loss to be no more than 10 % of the energy stored in the capacitor itself. Then we use the equations:
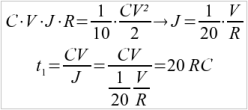
So with a charge time of 20 RC, and that is 4 times longer than with the constant voltage source, we reduced the amount of lost energy over the ESR to 10 %!
Of course, when we allow for a longer charge time, we can reduce the energy loss over the ESR evern more!
Other schemes
I showed two very different schemes to charge a capacitor and computed the results in energy loss over ESR. The most efficient one in energy loss is to use a current source and allow for a longer charge time. It is not always easy to make a constant current source, and perhaps a nice scheme that is between the two mentioned schemes is presented here:
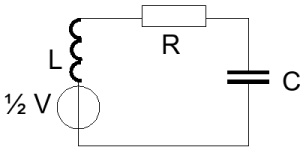
The way it works is as follows: you switch on the voltage source, to a value of 0.5 x V, when the capacitor C is empty. This results in an increasing current via the coil and ESR to the capacitor, and the current will charge the capacitor (also the current through the ESR R will result in energy loss). This current will not increase at the moment the voltage in the capacitor is equal to 0.5 x V. At that moment, it is the energy in the coil that ensures the current still continues to flow, but it will gradually decrease to zero. Now the charge on the capacitor is almost at a voltage V. We need to switch off the voltage source to prevent the charge in the capacitor (now at V volt) from flowing back to the voltage source. If we put a diode in the circuit, this will ensure that the current will not flow back. The current that has flown has a sinusoidal form (since we work with a capacitor and coil in series). To neglect the influence of the ESR, one has to make the value L of the coil as big as possible, and the value R of the ESR as low as possible, resulting in using thick wires and a lot of turns around a magnetically conducting core material. This scheme is possibly easier to make than a constant current source, when considering the high currents used for the super capacitor.




16 replies on “Charge Efficiency Capacitor”
Your formula’s are very impressive: haven’t seen anything like them since my school days, but they are well explained in your article. Excellent article!
Nice work … Thanks & Regards !!!
why do you intend to you use R in the circuit if its a contributor to energy losses?why can’t we use an LC Circuit?
Dear Nirveda,
It is not that I intend to use R, but the R in the “other schemes” paragraph, is the ESR (Equivalent Series Resistance) of the Capacitor C and the Coil L together. Therefore, the target is to make this R (being ESR) as low as possible. But you will anyhow have an R.
Dear Marcel, thanks for an interesting article… it’s good that ppl realise that charging a capacitor (and a water reservoir) is invariably a dissipative process, which leads to 50% of the energy becoming irretrievably ‘lost’. I think it would be the same even if somehow R=0, as there would then be an electromagnetic pulse (e.g. radio waves) of equal energy content. Like the click you hear on the radio when you turn the light on. This happens anyway during charging due to the dI/dt term, but is typically a small effect, as (in this case) is the dc magnetic term 1/2LI^2. The total dissipation would always add up to 50% of energy supplied (I think). Re your constant current charging, I feel you may not be comparing like with like in your illustration – as any real voltage source can be reconfigured to be a real current source (Thevenin to Norton), and vice-versa. The problem is a general one, and would apply also to pumped storage, see:
http://www.iop.org/EJ/article/0031-9120/33/5/018/pe8510.pdf?request-id=063291d9-13ae-4b19-bfee-e6d420d250ee
Hi Freaky,
Interesting point you make, by assuming/stating that 50 % energy is lost, also with the constant current. I do feel your statement to generalize it can be somewhat correct, however let’s take an example. The current power sources for computers use switching techniques to transfer (European) 230 V into 12 V or +5 or +3.3 V etc. This happens with an efficiency of 90+ percent! If that IS true, then I can make a current source as well with a high efficiency, hence preventing loss over R to be at 50 % of the total energy. I do believe the storage from energy or charge from grid voltage of 230 V into any capacitor of any voltage, is possible with an efficiency better than 50 %, when we take care that most of the charge does not have to pass the power supply capacitors but can be directly directed to the load. In such a case we do not loose energy over ESRs. Or would I still be mistaken’?
By the way, I was not able to follow your link (or I have to subscribe..)
Hi Marcel,
Yes the switching supplies are very efficient, because the capacitors have a very low ESR, and they do not continually charge and discharge, only the ripple voltage changes, and this is a few millivolts. The capacitors just remove ac components from the DC. A counter-example would be that energy companies (50 Hz AC) will charge extra to industry if they require a reactive load to be supplied (like the inductance of a lot of electric motors that are not PF corrected). The reactive power is itself not dissipative, but the power lines etc. used to supply it pass extra current and hence more power I^2*R is lost. The load can be either net capacitive or net inductive, both give this problem.
The constant current idea can alternatively be thought of as charging a capacitor from a constant voltage source V0 through a variable series resistor R that is altered with time, to precisely maintain a constant current I0 (it could be a depletion MOSFET for example, or any active load circuit, if you do not want to turn the knob towards R=0!). Say it takes a time tc to fully charge C to V0. The voltage rises linearly when current is constant, (from V=integral(I.dt)/C). The average power dissipated is thus 1/2(I0*V0) (a right-angled triangle) and the energy = 1/2(I0*V0)*tc. But from above, tc=C*V0/I0, and eliminating tc gives… (1/2)*C*V0^2! The energy stored in C is also (1/2)*C*V0^2, so the final situation is identical to charging through a constant R for infinite time. However, one important difference is that it occurs over a FINITE time, and is therefore much more useful!! Amplifiers designed to drive capacitive loads (like piezoelectric actuators) use this constant current charging technique to get good frequency response. The amplifier IS actually much more efficient, it dissipates about 1/10th of the power for the same charging voltage, at the same frequency. But sadly its maximum efficiency is… just 50%
Sorry about the link, it seems it’s on subscription. I got the pdf from a friend.
Freaky McSqueaky is absolutely right. Even assuming a current generator with active elements, the upper limit of energy efficiency is 50%. However, Marcel van der Steen should not be disappointed because even some senior scientists missed this issue, and that field is the “adiabatic charging” within “reversible computing”. The mistake is easy to see. The current generator must be driven by a battery of at least as high voltage U as the voltage of the fully charged capacitor at the end. At the beginning of the charging, the voltage drop on the current generator is equal to the battery voltage thus all the power U*I will heat the current generator. Because the sum of the voltages on the capacitor and the current generator is equal to the battery voltage, and the same current is flowing through both devices, the total power dissipation will always be U*I. The voltage will grow linearly on the capacitor and it is simple to make a drawing (U-I plot) where the areas show that in the idealized case 50% of the energy is lost in the current generator.
Good luck,
LK
Hey Guys,
Let me try to understand this. My statement in my article was that, only considering the capacitor and a constant current source, I can indeed limit the energy loss in the Capacitor’s ESR. So I suppose we all agree to that.
Then next, you focus on the constant current source, and include the efficiency of that current source into the total equation (I hope I am right and I understood your stories well now).
Well, if I understood your stories well, then you state that the constant current sources in combination with the charging of the capacitor will never be better than 50 % efficacy.
I still do not see this. For me, the efficacy/efficiency of a switched mode current supply can still be very high, assuming not a constant voltage source but a sinusoidal voltage source (which is the case nowadays) and the presented high efficiencies of higher than 80 % or even more.
So, assuming the 80 % of the (switched mode) current source, and a to be chosen efficiency of the charging of the capacitor (the lower the charge value, the better the efficiency as the ESR’s dissipation depends on IxIxR) we can still be better than the by you proposed 50 %.
What do you think?
Thanks,
Marcel.
Hi Marcel,
In your very first diagram you show a switch in series with your capacitor. You neglected this in your calculations. Ignoring the ESR, then the best power efficiency is 50%.
Think of it this way…
You need a certain charge transferred to charge the resistor. This means an initial Voltage accross the switch of the entire V, and a high current I. In this instantaneous state the power in the switch is VxI.
As the voltage increases the current decreases, and instantaneous power dissipation decreases.
If you follow this train of thought it is obvious there is power dissippated in the switch right up until the cap is fully charged (theoretically never).
Regards,
Colm
Hi Marcel,
Apologies for above typos (resistor instead of capacitor).
I just thought of the easiest way to explain this:
The law of ‘conservation of energy’ states that the total amount of energy in an isolated system remains constant.
If a capacitor starts with 0 energy (uncharged) and ends up with energy 0.5CV^2, then exactly that energy came from the voltage source expended accross the switch. Even an ideal switch gives you a weird maths problem with infinite currents and 0 resistance.
However (I think) if you introduce an inductor into your circuit you can transfer energy without having an IR voltage drop accross your switch, and in theory have perfect energy transfer.
I hope I have not caused any more confusion.
Regards,
Colm
Hi Colm,
In your reaction nr 10 you talk about the very first diagram. And there you say the efficiency is 50 %. And I fully agree, since with a constant voltage source and an empty capacitor that needs to be charged up to a voltage level the same as the source, one will loose 50 % of the total used energy to charge the capacitor. That is what is also shown with the equations.
But, charging with a constant current, one can improve its efficiency by reducing the constant current. The power loss in any ESR is proportional to I^2, and the charging time (and herewith also the energy loss) is only proportional to I^(-1). So finally, the energy loss is proportional to I, meaning the lower I, the lower the energy loss. So, only when assuming we have a constant current I to charge the capacitor, by choosing a lower constant value for I we can improve efficiency.
Now we can also look at how the constant current I is generated, and whether that generation of constant current I can be done with a high efficiency. I consider to use a switch mode constant current power supply of which there are types in the market with efficiencies up to 85 %. In this case, the multiplication of both efficiencies gives the total efficiency for charging a capacitor from a sinusiodal grid voltage via an efficient constant current source. My statement is that this can be accomplished with a total efficiency of over 50 %.
My comment to all above is as follows: A capacitor can be charged very efficiently using voltage steps. That is to arrange for several voltage steps as input to the capacitor. The time constant of C*R must be taken into account, and therefore the total charging time will increase with the number of steps. Used energy will be as given in the following example:
Charge supply voltage (V1): 12 Volts.
Used voltage steps: 6 Volts.
Number of steps: 2
Capacitor value: 1 Farad
Energy usage for step 1 is: (6*6*1)/2=18 Joules
Energy usage for step 2 is also 18 Joules
Total energy usage is: 36 Joules
(Compared to std voltage charging: (12*12*1)/2=72 Joules)
With only two steps we are using half the energy for charging the capacitor. Using more voltage steps give us
more reduction.
The stored energy in the capacitor is:
V1*V1*C = 12*12*1=144 Joules
(When charging time t=(CR*5)* Number of steps)
Does this also applies to batteries…. as you can see them as a big capacitor?
it depends whether the model of a battery is the same as the one for the capacitor: meaning whether a battery also has an ESR. I immagind that with a battery the max charging speed might be limited due to chemical processes and maybe that means that the ESR is not constant.
During capacitor charging or discharging whether the esr increase or decrease